Baansturing
Op welke wijze kan ik een traject rijden met mijn differential drive robot ?
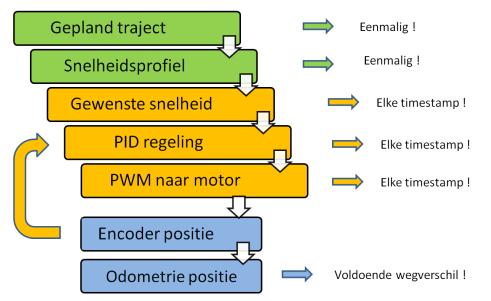
Goed, je eerste robot met PWM motor sturing en encoder is klaar. Op welke manier kan je nu met een zekere nauwkeurigheid bepaalde trajecten gaan afrijden ? In het volgende blokschema zie je de vereenvoudigde opbouw van het algoritme waar ik de voorkeur aan geef.
Gepland traject
Stel dat we een bepaalde afstand rechtdoor willen rijden met onze robot. Een aantal gegevens zijn dan nodig om dit traject te realiseren :
- De afstand die we willen afleggen (afstand in mm kan je omrekenen naar encodertics), voorwaarts of achterwaarts.
- De maximale snelheid waarmee we gaan rijden (wat is de maximale snelheid van je robot ?).
- De versnelling in het begin en de vertraging aan het einde van de beweging (wat is de ideale versnelling / vertraging van je robot ?).
- Het bewegingsprofiel dat we gaan gebruiken. Het meest gebruikt voor deze toepassing is het zogenaamde "trapezium" profiel.Dit wil zeggen dat de robot versnelt met een vaste versnelling tot aan de geplande maximale snelheid, en nadien weer afremt met een vaste vertraging tot aan stilstand.
Als we voor deze beweging een functie zouden schrijven, zou dit er zo kunnen uitzien :
move(max_snelheid,afstand,richting)
- max_snelheid is dan de maximale snelheid die tijdens dit traject mag bereikt worden
- afstand is de gewenste afstand die we willen afleggen, als deze afstand bereikt wordt moet de robot stilstaan !
- richting is dan voorwaarts of achterwaarts.
- De versnelling / vertraging houden we konstant voor alle bewegingen, deze moet dus niet als parameter van de functie doorgegeven worden.
- Deze functie wordt eenmalig opgeroepen als we de beweging willen starten, de vlag "beweging klaar" wordt laag gezet. Als de beweging uitgevoerd is, wordt de vlag "beweging klaar" terug hoog gezet. Op dit moment kan er terug een nieuwe beweging gestart worden.
Gewenst snelheidsprofiel
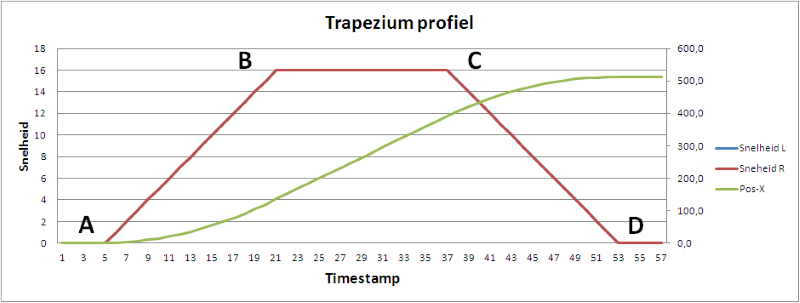
Op bovenstaande grafiek zie het geplande bewegingsprofiel. De rode lijn is de gewenste snelheid (in dit geval is de snelheid van linker en rechter motor exact gelijk, we willen immers rechtdoor rijden). De groene lijn is de afgelegde afstand. Er zijn 4 belangrijke punten te herkennen :
- Bij punt A start de beweging, op dat moment is de snelheid 0.
- Bij punt B wordt de maximale gewenste snelheid bereikt, vanaf nu rijden we verder met deze snelheid.
- Bij punt C beginnen we de snelheid terug af te bouwen.
- Bij punt D staat de robot terug stil, en hopelijk hebben we de juiste afstand afgelegd...
Belangrijke punten die worden berekend alvorens de beweging start!
Punt B
- Punt B lijkt eenvoudig, dat is immers de gewenste maximale snelheid. Maar, wat als de afstand zodanig kort is, dat we reeds moeten afremmen alvorens deze snelheid bereikt is ? Dit kunnen we te weten komen als we de afstand zouden kennen van het traject AB en het traject CD. De som van beide moet zeker kleiner zijn dan de gewenste afstand ! Welnu, een eenvoudige wiskundige formule geeft ons de afgelegde weg in functie van max.snelheid en versnelling:
afgelegde weg = 1/2*versnelling*tijd²
De tijd die nodig is om de max.snelheid te bereiken kan je berekenen door de maximale snelheid te delen door de versnelling. Uiteindelijk wordt de formule dan :
afgelegde weg= 1/2*max.snelheid²/versnelling
Als de versnelling en vertraging aan mekaar gelijk zijn, zullen ook de afstanden van traject AB en traject CD gelijk zijn ! Hieruit volgt dan dat de afstand minimaal gelijk moet zijn aan : minimale afstand = max.snelheid²/versnelling
Indien dus de af te leggen afstand kleiner is, moeten we de max. snelheid opnieuw berekenen. Dit kunnen we ook door de vorige formule te herleiden :
max.snelheid² = gewenste afstand/versnelling
Dus het punt B wordt op volgende wijze bekomen :
- Testen of de af te leggen afstand voldoende groot is, zodat de max.snelheid behaald wordt. Vanaf dan rijden we met een konstante snelheid verder tot aan punt C.
- Indien deze afstand kleiner is, moeten we de max.snelheid verminderen. Op het moment dat we dan deze snelheid bereiken, moeten we ogenblikkelijk terug gaan afremmen ! Er is dus geen fase met konstante snelheid, ons trapeziumprofiel is een driehoek geworden, punten B en C vallen samen !
Punt C
Punt C kunnen we ook afleiden uit de vorige formules. We kennen immers de afstand van het traject CD: afgelegde weg=1/2 max.snelheid²/vertraging Het punt C wordt dus de gewenste afstand verminderd met het traject CD. Vanaf dat punt beginnen we de snelheid terug af te bouwen.
Punt D
Dit is een makkie, bij punt D is de snelheid 0, en indien we een goede PID snelheidsregeling hebben, gaan we ook de gewenste afstand sterk benaderen ! Op dit moment kunnen we dus de vlag hoog zetten "einde beweging"
Welke eenheden moeten we gebruiken in ons programma ?
De normaal gebruikte eenheden voor in de wetenschap zijn :
- Afstand : De meter
- Tijd : sekonde.
- Snelheid : meter/sekonde
- Versnelling : meter /sekonde²
- Hoeken : radialen
Welnu, in ons programma zijn dit niet de meest geschikte eenheden omdat we dan gedwongen worden om met floats te werken. Veel meer voor de hand liggend zijn de eenheden die we daadwerkelijk meten met onze encoders. Bij mijn robot "Olimex3" heb ik volgende eenheden :
- Afstand : één encodertic (= ca 0.42 mm)
- Tijd : regellus wordt elke 100 ms doorlopen, één timestamp is dus 100 ms
- Snelheid : ecodertics /timestamp ( max snelheid vb 250 tics/100 ms)
- Versnelling : encodertics/timestamp² (ingestelde vb versnelling 20 tics/100ms²)
- Hoeken : encodertics
Deze werkwijze geeft het voordeel dat je het overgrote deel van de berekeningen kunt doen met integers. Voor odometrie is het wel noodzakelijk dat je de hoeken omrekent naar radialen omdat er goniometrische functies gebruikt worden. Omwille van praktische redenen kan je natuurlijk deze eenheden steeds omrekenen in je software. Het is bijvoorbeeld makkelijk als je een te rijden afstand kan ingeven als "mm".
Vereenvoudigd voorbeeld van C-code om één motor aan te sturen !
/*In deze move opdracht voor één motor worden volgende acties uitgevoerd :
1. Vlag beweging gestart wordt hoog gezet
2. De actuele tellerstand van de encoder wordt op 0 gezet (true_distance)
3. In functie van de gevraagde "distance" wordt er getest of "desired_speed" kan bereikt worden
4. Het rempunt (punt C) wordt berekend
5. Het eindpunt (pund D) wordt berekend
6. De gewenste maximale snelheid wordt in een variabele gezet.
Deze move opdracht wordt eenmalig opgeroepen, de verdere afhandeling van de beweging loopt dan in de functie
motion_control die telkens op een vaste "timestamp" herhaald wordt. In deze functie kan ook de PID regellus lopen
om de motorsnelheid te regelen !
*/
void move(int8_t desired_speed, uint8_t dir, uint16_t distance)
{
motion_status.move = true; //bewegingsvlag zetten
true_distance = 0; //actuele encoder teller op 0 zetten
uint16_t speed_max=sqrt(distance*speedramp); //max speed uitrekenen
if (desired_speed>speed_max) desired_speed=speed_max;//indien nodig snelheid begrenzen
preDecelerate = distance - (desired_speed*desired_speed)/speedramp/2; //afrempunt vastleggen
preStop = distance - 10; //nog iets voordien stoppen
max_desired_speed=desired_speed; //gewenste max. snelheid doorgeven
}
/* Deze functie wordt elke 100 ms uitgevoerd. Hierin wordt aan de hand van parameters die éénmalig door de "move" opdracht
zijn berekend, de gewenste actuele snelheid berekend. Via een PID regellus wordt deze snelheid dan zo nauwkeurig mogelijk geregeld.
Indien de beweging ten einde is, wordt de vlag "motion_status.move"terug laag gezet.
Uiteraard is er input nodig van de motor-encoder (m_speed is de actueel gemeten snelheid, dit is het aantal pulsen in de afgelopen 100ms.
De output is dan de PWM waarde die naar de motor gaat (m_power)
*/
void task_motionControl(void)
{
if(motor_control) {
motor_control=false; // wordt via timestamp elke 100 ms opnieuw hoog !!
//berekening gewenste snelheid
if(motion_status.move) {
if(true_distance >= preStop){ // Op tijd stoppen voor een betere nauwkeurigheid
m_desired_speed = 0;
max_left_des_speed = 0;
left_i = 0;
preStop_L = 0;
motion_status.move = false; //Vlag beweging is bezig wordt op 0 gezet.
}
else
if(true_distance >= preDecelerate) // Ramp vertragen indien afrempunt bereikt
m_desired_speed = m_desired_speed-decelerate;
else{
if(m_desired_speed < max_desired_speed) //Ramp versnellen indien max.snelheid nog niet bereikt
mleft_des_speed = mleft_des_speed + accelerate;
else mleft_des_speed = max_left_des_speed; // We hebben de max.snelheid bereikt
}
// PID motor speed control:
int16_t error = m_desired_speed - m_speed;//P-fout, m_speed is het aantal pulsen/100 ms
d_error = m_desired_speed -m_oldspeed; //D-fout
m_oldspeed = m_speed;
error_i = error_i + error; //I-fout
if(error_i > MC_IMAX) error_i = MC__IMAX;//anti windup
if(error_i < MC_IMIN) error_i = MC_IMIN;
//PWM aansturing
if (m_desired_speed>0)
m_power = 75+m_desired_speed*3+error_i - d_error + error*2; //PID regeling !!
else
m_power = -75+m_desired_speed*3+error_i - d_error + error*2; //PID regeling !!
}
}Een rekenmodel in excel met grafische voorstelling van de robotpositie !
De edele kunst van het rechtdoor rijden
Met onze PID regeling kunnen we nauwkeurig de snelheid van de motoren regelen. Als we dus rechtdoor willen rijden, moeten we er voor zorgen dat de snelheid van het linker en rechter wiel identiek zijn. In de praktijk zien we echter dat vooral tijdens het versnellen en vertragen van de motoren deze gelijkloop moeilijk te beheersen is. Het gevolg is dat tijdens deze fasen er toch ongewild lichte bochten gereden worden. Ook als beide motoren niet exact gelijk stoppen, wordt er in de afremfase nog afgeweken van de rechte lijn. Als we ons "E-Kompas" (dit is het verschil tussen linker en rechter encoder) bekijken, merken we dat er inderdaad een "hoekfout" optreedt tijdens de rit. Vooral bij het versnellen en het vertragen zien we deze hoekfout veranderen. De reden is dat onze PID-regeling een zekere vertraging vertoont om snelheidsfouten te kompenseren. Immers, het Integraal-aandeel is een som van opeenvolgende fouten, en dus opeenvolgende doorlopen van onze regeling. Stel dat we in de versnellende fase het L-wiel sneller draait dan het R-wiel. Onze PID-regeling gaat deze snelheidsfout wegregelen, maar het kwaad is dan al geschied : de hoekfout die is opgebouwd in deze fase blijft behouden bij het verder rechtdoor rijden. Een klassiek beeld is dus : We starten met een hoekfout 0, in de versnellende fase wordt er een hoekfout opgebouwd van enkele graden, bij konstante snelheid rijdt onze robot rechtdoor, maar wel met deze hoekfout ! In de afremmende fase wordt er dan weer een bijkomende hoekfout opgebouwd. Uiteindelijk heeft één motor de gewenste afstand bereikt, maar de andere motor draait dan nog even door. In het ideale geval wordt de hoekfout dan weer gekompenseerd. Het gevolg is dus een S-vormige baan. Een bijkomende regeling is dus gewenst !
De hoekfout wegregelen !
In onze klassieke PID snelheidsregeling wordt de regelafwijking van de motoren als volgt berekend :
Fout_L = Gewenste snelheid_L - Werkelijke snelheid_L Fout_R = Gewenste snelheid_R - Werkelijke snelheid_R
De richting (E_Kompas) die we rijden is echter ook bekend en bedraagt op elk moment :
E_Kompas = Werkelijke Afstand_L-Werkelijke Afstand_R
Als we dus rechtdoor willen rijden, moet ons E_Kompas in het ideale geval dus altijd 0 aangeven ! In werkelijkheid zal dit E_Kompas echter zelden 0 zijn. Als we nu de waarde van het E_Kompas mee in onze snelheidsregeling kunnen betrekken, is hier een grote verbetering te verwachten. Dit kan op een vrij eenvoudige wijze :
Fout_L = Gewenste snelheid_L - Werkelijke snelheid_L - P_Factor*E_Kompas Fout_R = Gewenste snelheid_R - Werkelijke snelheid_R + P_Factor*E_Kompas
De hoekfout gaat dus invloed uitoefenen op de snelheidsregeling van beide motoren, en wel zodanig dat de fout naar 0 geregeld wordt. Belangrijk is natuurlijk de "P_factor". Deze wordt zo ingesteld dat er een goede kompensatie is van de hoekfout, maar nog geen onstabiliteit van de regeling (kwispelen tijdens het rechtdoor rijden). Om bij grote hoekfouten een al te hevige reactie te voorkomen kan je ook nog eens de maximale waarde van P_Factor*E_Kompas beperken.
Een bepaalde richting aanhouden
Met deze regeling wordt het ook heel eenvoudig om een bepaalde richting aan te houden. Hiertoe definieren we de hoekfout als volgt :
E_Kompas = Werkelijke Afstand_L-Werkelijke Afstand_R+ Gewenste_Richting
De parameter "Gewenste_Richting" kan nu ten allen tijde gewijzigd worden, zelf tijdens het rijden ! De robot zal ogenblikkelijk reageren, en de nieuwe "Gewenste_Richting" volgen ! Om al te hevige richtingscorrecties te vermijden, is het hier zeker belangrijk om de maximale waarde van P_Factor*E_Kompas te beperken.
Nog enkele tips
- De resolutie van de wielencoders is hier erg belangrijk : in de praktijk kan je de hoekfout wegregelen tot ca +/- 3 encodertics. Bij een grove resolutie van 1°/tic zal je dus nog steeds een aanzienlijke hoekfout hebben. Deze resolutie wordt berekend als volgt (Vb mijn Discovery robot):
Spoorbreedte = 187 mm Encoder resolutie = 0.0705 mm/tic E_compass : 187mm*2*PI/0.0705 = 16666 tics/360° E_compass resolutie = 46.29 tics/graad
- De P-factor kan je ook nog afhankelijk maken van de gereden snelheid : immers, bij een vaste P-factor zal de reactie op een hoekfout altijd een vaste "snelheids-correctie" opleveren. Bij langzaam rijden zie je dan een grote reactie, en mogelijk zelfs oscillatie, en bij snel rijden is de reactie eerder sloom te noemen.
- Bij samengestelde trajecten is het belangrijk dat je steeds de waarde van het E-Kompas bijhoudt. Dus zeker niet bij elke nieuwe rij-opdracht je E_Kompas terug op 0 zetten ! Het mooie van zo een odometrie kompas is net dat de theoretische richting altijd behouden blijft, zelfs na de meest gekke bochten !
Bochten rijden met een differential drive robot
Simulatie : Media:Odometrie_bocht.xlsx
De cirkelboog
Een bocht rijden lijkt de eenvoud zelve : zorg ervoor dat de snelheid van het linker en rechter wiel verschillend zijn ! Een bocht rijden met een vooraf geplande baan is ietwat moeilijker, en hiervoor moeten we eerst het wiskundig verband kennen tussen de bochtstraal en de wielsnelheden. Gelukkig is dit verband zeer eenvoudig : De bochtstraal is recht evenredig met de verhouding van wielsnelheden ! Uiteraard is ook de wielbasis hier van belang, en deze komt dan ook voor in de formule. Deze functie geeft de bochtstraal tov het center van de wielbasis :
Bochtstraal = Wielbasis*(Wielsnelheid_L+Wielsnelheid_R)/2*(Wielsnelheid_L-Wielsnelheid_R)
Opgelet, afhankelijk van welk wiel het snelste draait kan de bochtstraal hier negatief zijn. Om het een en het ander visueel voor te stellen heb ik hiervoor een spreadsheet opgesteld. Als eerste voorbeeld gaan we een bocht van 300° rijden met een bochtstraal van 170 mm. We vertrekken vanuit stilstand, het linker wiel krijgt een versnelling van 0.6 tics/s², rechts stellen we 1.2 tics/s² in. Ook hier houden we een mooi trapeziumprofiel aan, dus ook vertragen met dezelfde snelheidsprofielen. Het resultaat is een perfecte cirkelboog van ca 310° !
Belangrijk : om een cirkelboog met een constante straal te rijden MOET de verhouding tussen de snelheid van Linker en Rechter wiel constant zijn ! Dit kan nooit bereikt worden als de beweging start met een bepaalde beginsnelheid van de robot. Als de beweging start vanuit stilstand is dit wel mogelijk, maar ook dan moet de versnelling / vertraging van het Linker en Rechter wiel dezelfde verhouding hebben als de gewenste eindsnelheden.
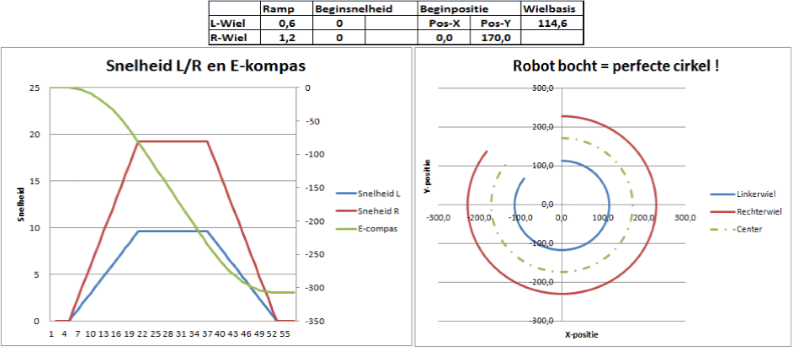
De boog, maar met gelijke versnelling L/R wiel
Hier hebben we een identiek versnelling L/R gekozen, maar de versnelling/vertraging van het R-wiel blijft langer duren. De kromme is inderdaag geen cirkel meer. Zowel in het begin als aan het einde zien we een lineair gedeelte, daarna zien we weer een spiraal vorm.
Bocht vanuit een bepaalde beginsnelheid
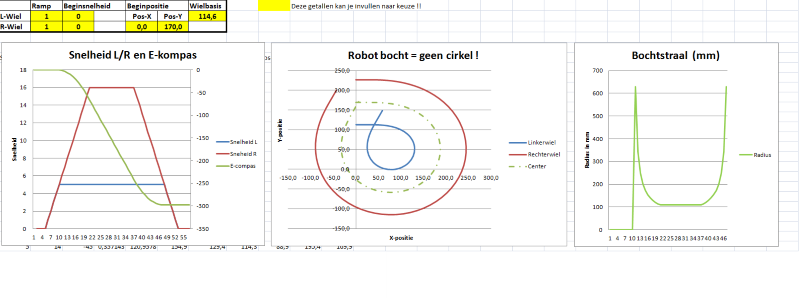
Onze tweede simulatie echter moet wat vlotter verlopen, dus we vertrekken vanuit een bepaalde beginsnelheid !! En wat blijkt : de perfecte cirkelboog is verdwenen ! Het gebied waar de robot versnelt en vertraagd is allesbehalve cirkelvormig, het lijkt eerder een stuk van een spiraal vorm. Waar de snelheid konstant is, herkennen we nog wel de cirkelvorm. De oorzaak ligt in het feit dat de verhoudingen van de wielsnelheden niet meer constant zijn in de versnellende/vertragende fase ! Dit kan je niet oplossen door een ander snelheidsprofiel te kiezen ! Indien je een bocht start vanuit een bepaalde beginsnelheid, zal je altijd een dergelijke spiraalvorm rijden ! De enige manier om een exacte cirkelboog te rijden, is starten vanuit stilstand. Overigens worden treinbochten en op/afritten van wegen ook via een dergelijke kromme aangelegd. De wiskundige benaming is de "clotoide".
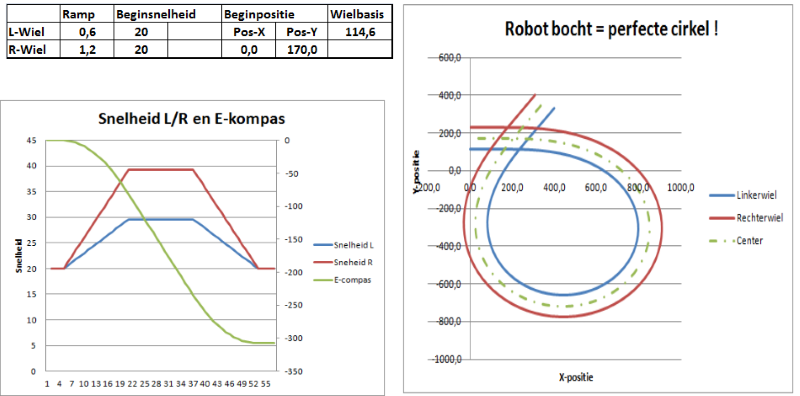
Bocht vanuit ter plaatse draaien
Nu nog een derde simulatie, die start vanuit "ter plaatse draaien". Hier is ook de grafiek van de bochtstraal bijgevoegd :
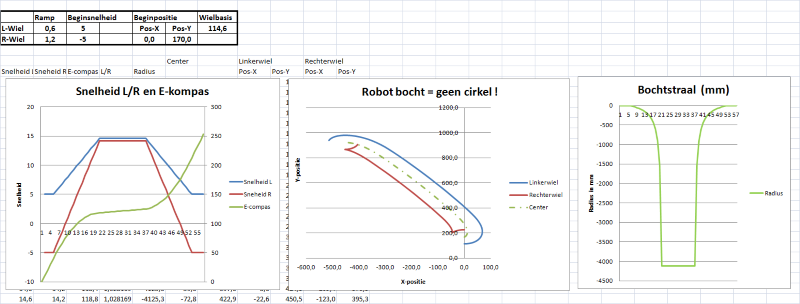
Een bocht traject met een bepaalde hoek en een bepaalde straal rijden
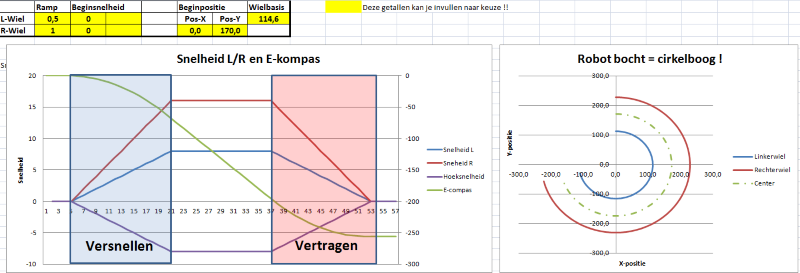
Dit is inderdaad mogelijk als we rekening houden met voorgaande beperkingen. De straal van onze bocht is dus afhankelijk van de verhouding van de wielsnelheden. Als we dus een perfecte cirkelboog willen rijden, moet deze verhouding ten alle tijden constant zijn. Vanuit stilstand is dit altijd mogelijk, als we reeds bewegen is dit meestal niet mogelijk. De bocht kan wel gereden worden, maar het zal dan geen perfecte cirkelboog zijn. Ik gebruik het volgend algoritme :
- 1. Kies de wielsnelheid links en rechts in functie van de bochtstraal. De verhouding bepaalt dus de bochtstraal, en de som van de absolute snelheden bepaald de gemiddelde snelheid van de robot. Als je ter plaatse wil draaien, zijn de snelheden L/R gelijk, maar tegengesteld.
- 2. Bereken de versnelling/vertraging van elk wiel apart, naargelang de gewenste eindsnelheid van elk wiel. Stel dat je standaard een versnelling gebruikt van 10 tics/s², en je wil nu een eindsnelheid links van 100 tics/s en rechts van 200 tics/s. Als je nu links een versnelling kiest van 5 tics/s² en rechts 10 tics/s² zal je steeds een constante verhouding van wielsnelheden hebben. Je rijdt dan een perfecte cirkelboog, en de gewenste eindsnelheden zullen op hetzelfde tijdstip bereikt worden. Ook bij het afremmen geldt dit, beide wielen zullen op hetzelfde tijdstip snelheid 0 terug bereiken.
- 3. Bereken het punt dat je terug moet beginnen afremmen. Voor een rechtlijnige beweging is dat na een bepaalde afgelegde afstand (zie het begin van dit artikel). Voor een perfecte cirkelboog zou je eventueel de lengte van de cirkelboog kunnen berekenen, en ook na een bepaalde afstand terug beginnen af te remmen. Maar er is ook een andere manier, die universeler is : bereken bij welke waarde van het E-kompas je moet beginnen af te remmen !! Eigenlijk is de werkwijze identiek aan het algoritme om een bepaalde afstand af te leggen, maar nu gebruik de waarde van het E-kompas !
- 4. hoekverdraaing =1/2 max.draaisnelheid²/gemiddelde hoeksnelheidvertraging
Dit is dus de hoekverdraaing dat de robot nog zal rijden in de afremmende fase. De "max.draaisnelheid" is hier gewoon snelheidL-snelheidR. De gemiddelde hoeksnelheidvertraging is hier (vertragingL-vertragingR). In de onderstaande figuur zie je weer de verschillende fases van de beweging.
- De eerste fase is de versnellende fase, de hoeksnelheid neemt toe met een hoekversnelling die het verschil is van de de wielversnelling Links en Rechts ! De verandering van het E-kompas kan je hier dus berekenen met de formule hoek = 1/2 max.hoeksnelheid²/hoekversnelling
- Daarna komen in de fase van constante snelheid, en ook dus een constante hoeksnelheid. Deze hoeksnelheid is wederom "het verschil van de wielsnelheid Links en Rechts". De hoek die hier afgelegd wordt is eenvoudig te berekenen : hoek= hoeksnelheid*tijd
- De laatste fase is het afremmen, eigenlijk identiek aan de versnelfase, maar dan met een "hoekvertraging". Ook hier is de formule identiek aan de versnelfase, maar nu is het teken van de hoekversnelling omgekeerd ! hoek = 1/2 max.hoeksnelheid²/hoekvertraging
Tot slot nog een video waarin de resultaten van dit bochtenwerk zichtbaar is :